【完稿】液体灌装生产线上拧瓶盖机的设计【CAD定稿】

格式：RAR 上传：2022-06-25 13:10:43

《【完稿】液体灌装生产线上拧瓶盖机的设计【CAD定稿】》修改意见稿

1、“.....则它们构成曲面在点的切平面上的坐标系。我们给出曲面上点的个方向，设是对应于方向的法曲率，为法曲率半径的绝对值。过点沿方向即画线段，使其长度等于，则对于切平面上所有的方向，点的轨迹成为曲面在点的迪潘指标线。迪潘指标线的方程为上式中的系数与曲面上的方向无关，它们对于曲面上已知点来说即为常数，并且上式中不含，的次项，所以上述方程表示以为中心的有心二次曲线。这样，曲面上的点由它的迪潘指标线可以进行分类如果，则点成为曲面的椭圆点，这时迪潘指标线是椭圆如果，则点成为曲面的双曲点，这时迪潘指标线是对双曲线。如果，则点成为曲面的抛物点，这时迪潘指标然后以曲面的第，第二基本形式，法曲率，迪潘指标线共轭方向为基础下讨论了曲面的主方向。最后用具体地例子来研究了二次曲线的主方向和曲面的主方向的联系。关键词二次曲线主方向特征根迪潘指标线曲面主曲率引言解析几何是大学数学系的主要基础课程之......”。

2、“.....所以这两门课程的内容有着密切的关系。本文章的主要目的也是讨论解析几何中的“二次曲线的主方向”和微分几何中的“曲面的主方向”及其它们的联系。本文章论证严谨，同时又力求简明，叙述上深入浅出，条理清楚，让读者很容易掌握里面的内容。二次曲线的主方向定义为二次曲线,的非渐近方向，若共轭与该方向的直径与方向垂直，则称这直径为二次曲线的主直径而直径方向及方向均成为二次曲线的主方向。主直径是二次曲线的对称轴，因此主直径也叫做二次曲线的轴。如果二次曲线为中心曲线，那么根据主方向的定义非渐近方向为主方向与共轭方向垂直因此成为中心二次曲线的主方向的条件是成立，其中，或把它改写成可见，这是个关于,的齐次线性方程组，而,不能全为零。所以即可见，若求二次曲线,的主方向,只需先求方程式的根，再代入式就能得到它的主方向。如果二次曲线为非中心二次曲线......”。

3、“.....即式中的可取等于零，这样当时，方程式的两根为，把它代入式所得的主方向，正是非中心二次曲线的渐近主方向与非中心二次曲线主方向。定义方程式成为二次曲线的特征方程，其根成为曲线的特征根。性质二次曲线的特征根全为实数事实上，二次曲线的特征根不全为零。事实上，若不然，则即所以这不可能定理主方向为渐近主方向对应与方向的特征根为......”。

4、“.....讨论它们的联系为目的而进行的。也就是说，本文章首先讨论了二次曲线的定义，它的求法，特征方程和特征根。然向。在脐点处可设，设是脐点处任方向，而是它的垂直方向，这时两边乘以，得因此与也共轭，是对主方向。因此脐点处任意方向为主方向。主方向的判别定理是主方向的充要条件是存在实数，使这时是方向的法曲率，也是这点的主曲率。二次曲线的主方向和曲面的主方向的联系曲面在椭圆点的迪潘指标线是曲面在该点的切平面上的椭圆，曲面此点对主方向是该椭圆的对主直径即对称轴的方向。曲面在双曲点的迪潘指标线是曲面该点的切平面上的双曲线，曲面此点的对主方向是该双曲线的对主直径即对称轴的方向。曲面在抛物点的迪潘指标线是曲面在该点的切平面上的对平行直线，曲面此点的对主方向是该平行直线的对主直径即对称轴的方向。曲面在平点没有迪潘指标线，曲面在平点处的每个方向都是主方向。总之......”。

5、“.....它们也是这点的迪潘指标线二次曲线的主轴方向。总结综上所述，本文章主要讨论了二次曲线的主方向和曲面的主方向及其它们的联系。为了达到目的，首先讨论了二次曲线的主方向概念，它的求法，特征方程和特征根。然后以曲面第，第二基本形式，迪潘指标线来讨论了曲面的主方向。最后以上内容基础下，研究了二次曲线的主方向和曲面的主方向的联系。通过这些分析和研究，我们得到这样个结论是对平主方向的充要条件是存在实数，使这时是方向的法曲率，也是这点的主曲率。二次曲线的主方向和曲面的主方向的联系曲面在椭圆点的迪潘指标线是曲面在该点的切平面上的椭圆，曲面此点对主方向是该椭圆的对主直径即对称轴的方向。曲面在双曲点的迪潘指标线是曲面该点的切平面上的双曲线，曲面此点的对主方向是该双曲线的对主直径即对称轴的方向。曲面在抛物点的迪潘指标线是曲面在该点的切平面上的对平行直线，曲面此点的对主方向是该平行直线的对主直径即对称轴的方向。曲面在平点没有迪潘指标线......”。

6、“.....总之，曲面上每点处除了平点之外总有两个方向，它们也是这点的迪潘指标线二次曲线的主轴方向。总结综上所述，本文章主要讨论了二次曲线的主方向和曲面的主方向及其它们的联系。为了达到目的，首先讨论了二次曲线的主方向概念，它的求法，特征方程和特征根。然后以曲面第，第二基本形式，迪潘指标线来讨论了曲面的主方向。最后以上内容基础下，研究了二次曲线的主方向和曲面的主方向的联系。通过这些分析和研究，我们得到这样个结论即曲面上点除了平点之外的主方向是曲面该到的迪潘指标线二次曲线的主轴方向。参考文献吕林根等编解析几何第三版北京高等教育出版社,梅向明，黄敬之编微分几何第四版北京高等教育出版社,周建伟微分几何北京高等教育出版社，梅向明等编微分几何学习指导与习题选节北京高等教育出版社，周建伟编解析几何北京高等教育出版社,吕林根解析几何学习辅导书北京高等教育出版社梅向明，黄敬之编微分几何第二版北京高等教育出版社,致谢大学五年很快就要结束了，在这宝贵的五年学习过程中......”。

7、“.....得到了他们热心的帮助和关心，使我能够顺利的完成学业，同时我的道德修养在身边优秀的老师和同学的感染下得到了很大的提高，在此向他们表示我最衷心的感谢！在老师的指导下我的毕业论文顺利通过，她帮我批阅了好多次，提供了这方面的资料和很好的意见，非常感谢她的帮助，在老师耐心的指导下，我学会了论文的三步骤怎么样开头，怎么样继续，怎么样结束。非常感谢指导老师，也非常感谢我系的各位老师，在她们的教育下，我在各方面得到了很大的提高，为以后工作打下了良好的基础。此致敬礼古丽努尔艾麦提年月证设主方向对应的特征根为，所以因为,全为实数，且不全为零所以,定理中心二次曲线至少有两条主直径，具体地，圆的任意实直径均为主直径，非圆的中心曲线仅有两条即相垂直又相共轭的主直径无心二次曲线只有条主直径。线心曲线的主直径就是唯的主直径，赤即中心直线或渐近线。曲面的主方向设，是个曲面......”。

8、“.....是,的可微函数，也可以看成曲面上的函数。定义称是曲面的第基本形式，是曲面的第基本量。曲面的第基本形式也叫做曲面的弧长元素，可以用来计算曲面上曲线的弧长，曲面上区域的面积及曲面上两曲线的夹角等。定义称是曲面的第二基本形式，其系数，,是曲面上的函数，成为曲面的第二基本量。第二基本形式反映曲面在点附近沿方向的是对平行直线。如果，则点成为曲面的平点平面上的点都是平点,这时迪潘指标线不存在。设曲面上点处的两个方向为和，如果包含这两个方向的直线是点的迪潘指标线的共轭直径，则方向和成为曲面的共轭方向。定义曲面上点的两个方向，如果它们即正交又共轭，则称为曲面的主方向，主方向对应的法曲率称为曲面的主曲率。由定义知道，主方向总是成对出现的。与是对主方向的条件也可以表示为......”。

9、“.....如果不全为零，称这种脐点为曲面上的圆点。推论脐点处任方向为主方向，对应的主曲率是常数，在圆点处此常数不为零非脐点处有且只有对主方向，这两个主方向互相共轭垂直。证在非脐点处，主方向的方程为，主方向方程的解与垂直的条件是它显然成立，同理可知与共轭的条件是它也显然成立，因此曲面在非脐点处只有对主方曲情况，它也告诉我们在这方向朝切平面的那边弯曲。定义称Ⅱ是曲面沿方向的法曲率。通过曲面上点,作平行于法矢及方向的平面，它与曲面交与条曲线，叫做处沿方向法载线。性质设是沿方向的法曲率，是法载线在处的曲率，在时时，法载线向方向弯曲时，法载线向相反方向弯曲定义我们取点为原点......”。

本资源为压缩包，下载后将获得以下全套资料（图纸+论文+其他）

13 m10 luoshuan 3.prt

a1.prt a1.prt

A11.prt A11.prt

A12.prt A12.prt

a2.prt a2.prt

a3.prt a3.prt

a4.prt a4.prt

a5.prt a5.prt

a7.prt a7.prt

a8.prt a8.prt

a9.prt a9.prt

chilun2.prt

chilunda360.prt

chilunxiao60.prt

chulun11.prt

dailunda140.prt

dailunxiao70.prt

dangban1.prt

dangban2.prt

dangban3.prt

dangban5.prt

dangban7.prt

dangban8.prt

dangban9.prt

dianji.prt

dianji1.prt

dianji2.prt

dianji3.prt

dianji4.prt

dianji5.prt

dianji7.prt

dianji9.prt

jian47.prt

jian52.prt

ligaiji1.prt

ligaiji2.prt

ligaiji3.prt

ligaiji4.prt

ligaiji5.prt

ligaiji6.prt

ligaiji7.prt

pinggai.prt

pingzi.prt

shengjiang1.prt

shengjiang10.prt

shengjiang11.prt

shengjiang3.prt

shengjiang4.prt

shengjiang5.prt

shengjiang6.prt

shengjiang7.prt

shengjiang8.prt

shengjiang9.prt

xiangzuo.prt

xiangzuo1.prt

xiechilun.prt

xiechilun1.prt

xiechilun2.prt

yuanzhuzhoucheng1.prt

yuanzhuzhoucheng2.prt

zhicheng1.prt

zhoucheng xiao.prt zhoucheng xiao.prt

zhoucheng.prt

zhoucheng1.prt

zhoucheng2.prt

zhoucheng3.prt

zhoucheng4.prt

zhuangpan4.prt

zhuangpan5.prt

zhuanpan1.prt

zhuanpan2.prt

zhuanpan3.prt

zhuichilunda.prt

zhuichilunxiao.prt

zhuzhou.prt

zhuzhoutuzhi.prt

大齿轮.dwg （CAD图纸）

大齿轮.pdf

大带轮.dwg （CAD图纸）

大带轮.pdf

大锥齿轮.dwg （CAD图纸）

大锥齿轮.pdf

计划周记进度检查表.xls

开题报告.doc

任务书.doc

设计说明书（论文）.doc

外文翻译.doc

小齿轮.dwg （CAD图纸）

小齿轮.pdf

小带轮.dwg （CAD图纸）

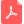小带轮.pdf

小锥齿轮.dwg （CAD图纸）

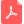小锥齿轮.pdf

主轴.dwg （CAD图纸）

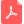主轴.pdf

转盘.dwg （CAD图纸）

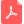转盘.pdf

总装图.dwg （CAD图纸）

总装图.pdf

仅支持预览图纸，请谨慎下载！

Hi，我是你的文档小助手!

你可以按格式查找相似内容哟

DOC PPT RAR 精品全部

小贴士：

🔯 当前文档为RAR文档，建议你点击RAR查看当前文档的相似文档。
⭐ 查询的内容是以当前文档的标题进行精准匹配找到的结果，如果你对结果不满意，可以在顶部的搜索输入框输入关健词进行。